Gia H. Ngo, Meenakshi Khosla, Keith Jamison, Amy Kuceyeski, Mert R. Sabuncu

Abstract

Resting-state functional MRI (rsfMRI) yields functional connectomes that can serve as cognitive fingerprints of individuals. Connectomic fingerprints have proven useful in many machine learning tasks, such as predicting subject-specific behavioral traits or task-evoked activity. In this work, we propose a surface-based convolutional neural network (BrainSurfCNN) model to predict individual task contrasts from their resting-state fingerprints. We introduce a reconstructive-contrastive loss that enforces subject-specificity of model outputs while minimizing predictive error. The proposed approach significantly improves the accuracy of predicted contrasts over a well-established baseline. Furthermore, BrainSurfCNN’s prediction also surpasses test-retest benchmark in a subject identification task.

Overview

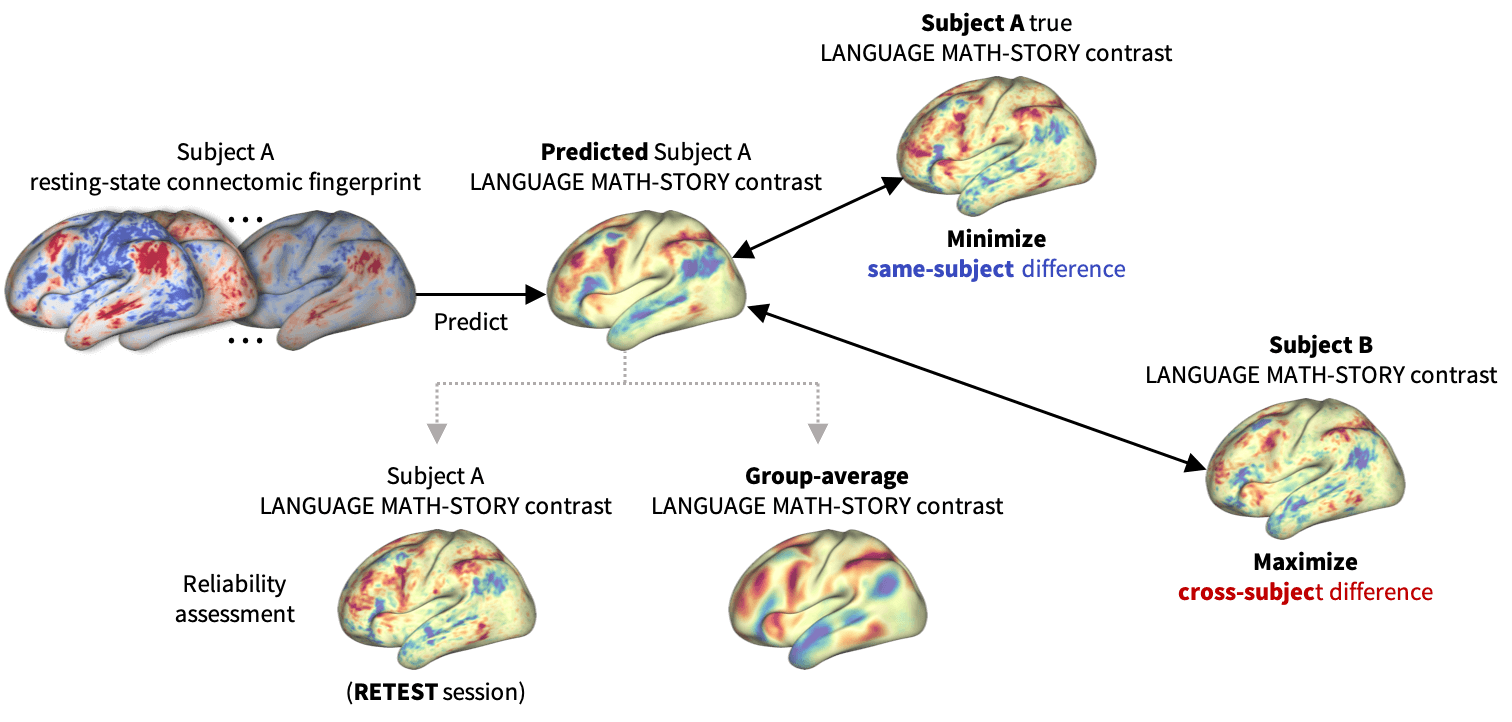overview Figure 1: BrainSurfCNN learns to predict an individual task contrast from their surface-based functional connectome by optimizing two objectives - minimizing the predictive error \(L_R\) while maximizing the average difference \(L_C\) with other subjects.

Functional connectomes derived from resting-state functional MRI (rsfMRI) carry the promise of being inherent “fingerprints” of individual cognitive functions (Biswal et al., 2010). Such cognitive fingerprints have been used in many machine-learning applications (Khosla et al., 2019), such as predicting individual developmental trajectories (Dosenbach et al., 2010), behavioral traits (Finn et al., 2015), or task-induced brain activities (Tavor et al., 2016, Cole et al., 2016). In this work, we propose BrainSurfCNN, a surface-based convolutional neural network for predicting individual task fMRI (tfMRI) contrasts from their corresponding resting-state connectomes. Figure 1 gives an overview of our approach: BrainSurfCNN minimizes prediction’s error with respect to the subject’s true contrast map, while maximizing subject identifiability of the predicted contrast.

Convolutional neural networks (CNNs) were previously used for prediction of disease status from functional connectomes (Khosla et al., 2019), albeit in volumetric space. Instead, we used a new convolutional operator (Jiang et al., 2019) suited for icosahedral meshes, which are commonly used to represent the brain cortex. Working directly on the surface mesh circumvents resampling to volumetric space with unavoidable mapping errors. Graph CNN is also closely related to mesh-based CNN, but there is no consensus on how pooling operates in unconstrained graphs. In contrast, an icosahedral mesh is generated by regular subdivision of faces from a mesh of a lower resolution, making pooling straightforward.

BrainSurfCNN Architecture

model

Figure 2: BrainSurfCNN Architecture

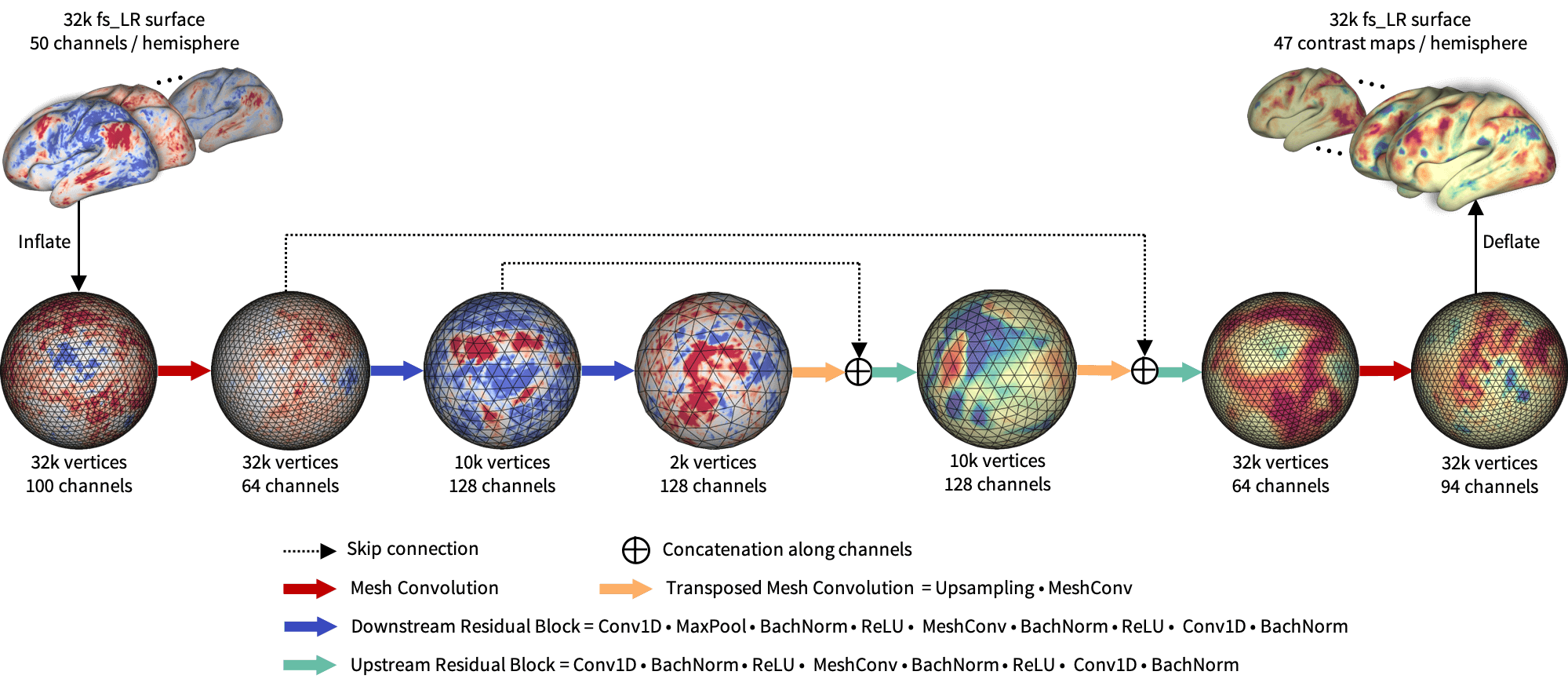
Figure 2 shows the proposed BrainSurfCNN model for predicting task contrasts from rsfMRI-derived connectomes. The model is based on the popular U-Net architecture (Ronneberger et al., 2015) using the spherical convolutional kernel proposed in (Jiang et al., 2019). Input to the model is surface-based functional connectomes, represented as a multi-channel icosahedral mesh. Each input channel is a functional connectivity feature, for example, the Pearson’s correlation between each vertex’s timeseries and the average timeseries within a target ROI. In our experiments, the subject-specific target ROIs were derived from dual-regression of group-level independent component analysis (ICA) (Smith et al., 2013).

The input and output surface meshes are fs_LR meshes (Van Essen et al., 2012) with 32,492 vertices (fs_LR 32k surface) per brain hemisphere. The fs_LR atlases are symmetric between the left and right hemispheres, e.g., the same vertex index in the both hemi-spheres correspond to cotra-lateral analogues. Thus, each subject’s connectomes from the two hemispheres can be concatenated, resulting in a single input icosahedral mesh with the number of channels equals twice the number of ROIs. BrainSurfCNN’s output is also a multi-channel icosahedral mesh, in which each channel corresponds to one fMRI task contrast. This multi-task prediction setting promotes weight sharing across contrast predictions.

Data

We used the minimally pre-processed, FIX-cleaned 3-Tesla resting-state fMRI (rsfMRI) and task fMRI (tfMRI) data from the Human Connectome Project (HCP). rsfMRI data was acquired in four 15-minute runs, with 1,200 time-points per run per subject. HCP also released the average timeseries of independent components derived from group-level ICA for individual subjects. We used the 50-component ICA timeseries data for computing the functional connectomes. HCP’s tfMRI data comprises of 86 contrasts from 7 task domains (Barch et al., 2013), namely: WM (working memory), GAMBLING, MOTOR, LANGUAGE, SOCIAL RELATIONAL, and EMOTION. Redundant negative contrasts were excluded, resulting in 47 unique contrasts.

HCP released 3T imaging data of 1200 subjects, out of which 46 subjects also have retest (second visit) data. By considering only subjects with all 4 rsfMRI runs and 47 tfMRI contrasts, our experiments included 919 subjects for training/validation and held out 39 test-retest subjects for evaluation.

Reconstructive-Contrastive Loss

Given a mini batch of \(N\) samples \(B = \{\mathbf{x}_i\}\), in which \(\mathbf{x}_i\) is the target multi-contrast image of subject \(i\), let \(\hat{\mathbf{x}}_i\) denote the corresponding predicted contrast image. The reconstructive-contrastive loss (R-C loss) is given by:

\[\mathcal{L}_R = \frac{1}{N}\sum_{i=1}^{N}d(\hat{\mathbf{x}}_i, \mathbf{x}_i)\] \[\mathcal{L}_C = \frac{1}{(N^2-N)/2}\sum_{\substack{\mathbf{x}_j\in{B_i}\\ j\neq{i}}}d(\hat{\mathbf{x}}_i, \mathbf{x}_j)\] \[\mathcal{L}_{RC} = \left[\mathcal{L}_R-\alpha\right]_{+} + \left[\mathcal{L}_R - \mathcal{L}_C + \beta\right]_{+}\]

where \(d(.)\) is a loss function (e.g. \(l^2\)-norm). \(\mathcal{L}_R\), \(\alpha\) are the same-subject (reconstructive) loss and margin, respectively. \(\mathcal{L}_C\), \(\beta\) are the across-subject (contrastive) loss and margin, respectively.

The combined objective enforces the same-subject error \(\mathcal{L}_R\) to be within \(\alpha\) margin, while encouraging the average across-subject difference \(\mathcal{L}_C\) to be large such that \(\left(\mathcal{L}_C - \mathcal{L}_R\right) > \beta\).

Results

Contrasts prediction quality

prediction_quality 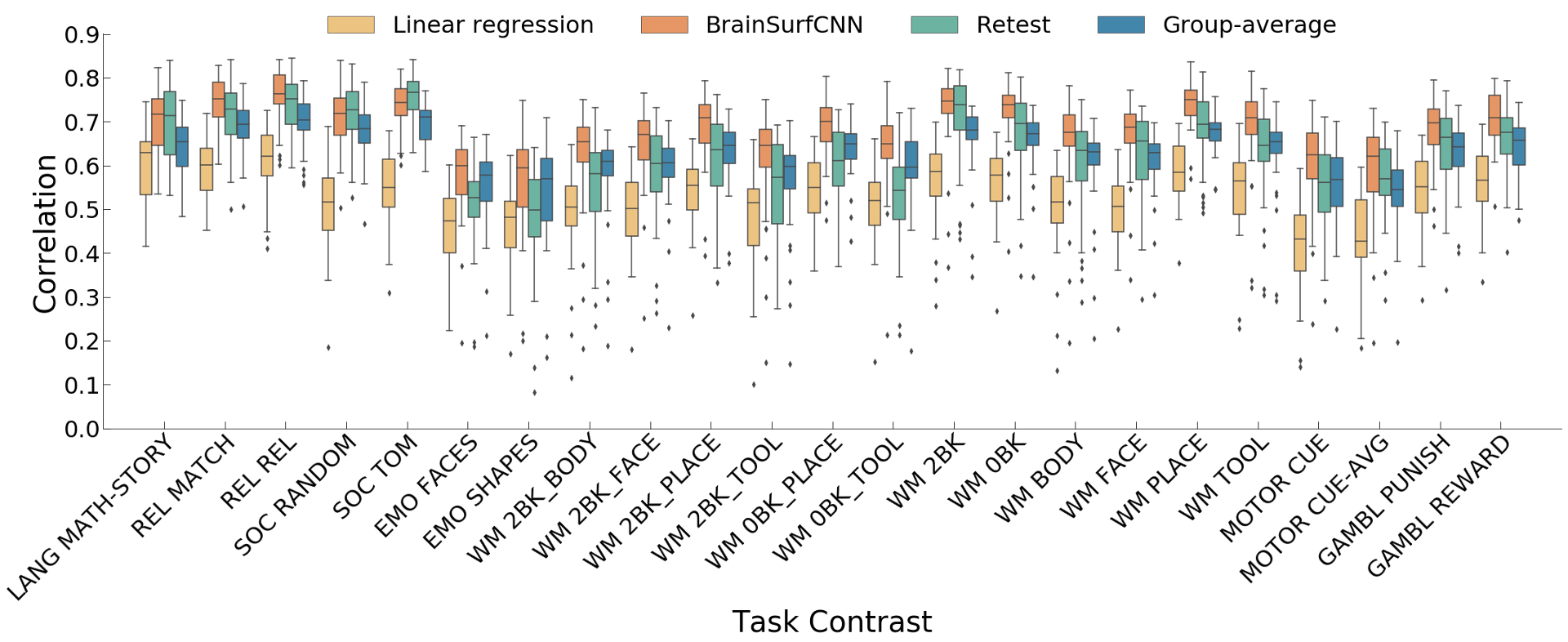Figure 3: Correlation of predicted with true individual task contrasts (only reliable contrasts are shown). LANG, REL, SOC, EMO, WM, and GAMBL are short for LANGUAGE, RELATIONAL, SOCIAL, EMOTION, WORKING MEMORY and GAMBLING respectively.

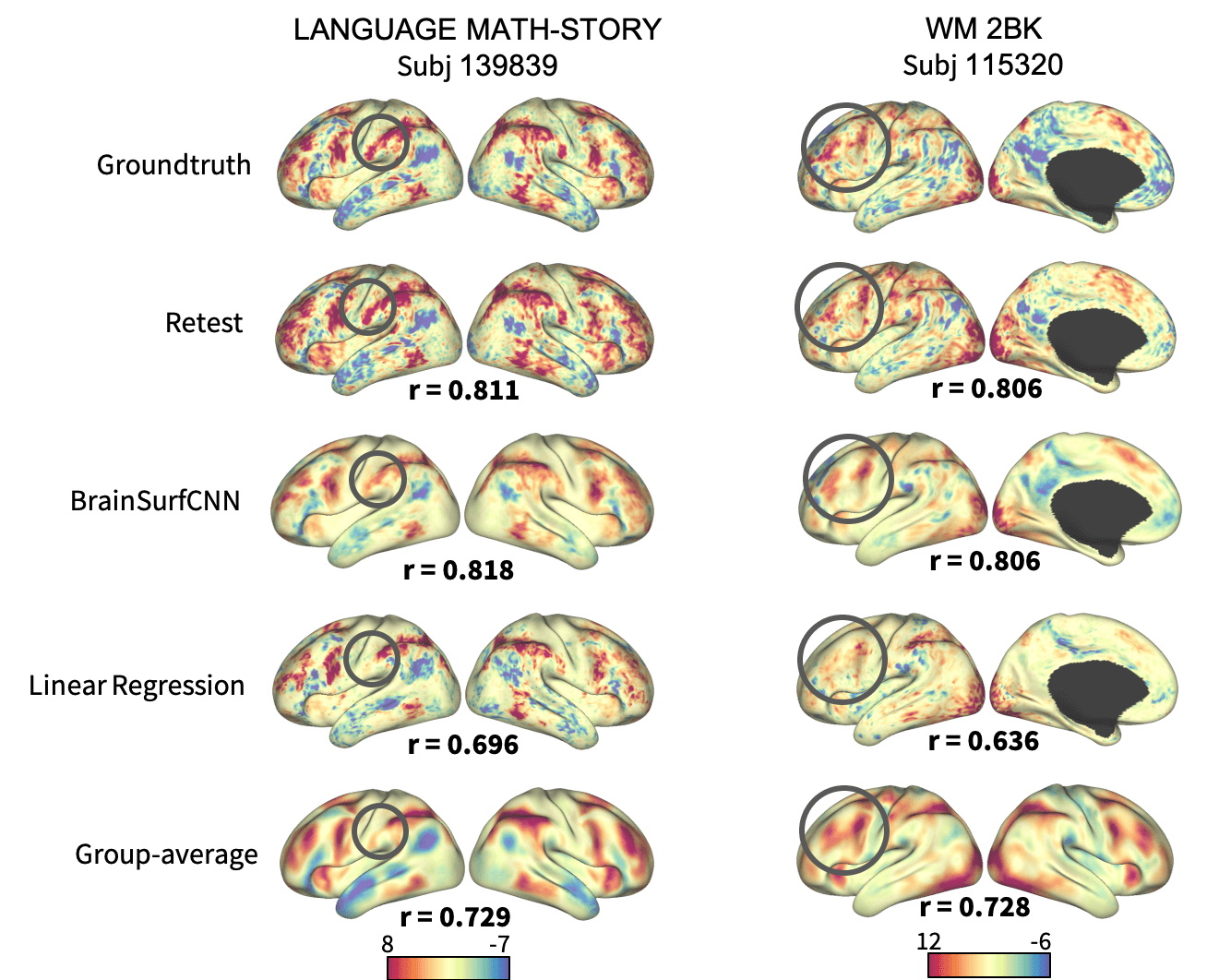example Figure 4: Surface visualization for 2 task contrasts of 2 subjects. The right-most column shows the group-average contrasts for comparison.

Figure 3 shows the correlation of models’ prediction with the same subject’s observed contrast maps. Only reliably predictable task contrasts, defined as those whose average test-retest correlation across all test subjects is greater than the average across all subjects and contrasts, are shown in subsequent figures. Figure 4 shows the surface visualization of 2 task contrasts for 2 subjects. While the group-average match individual contrasts’ coarse pattern, subject-specific contrasts exhibit fine details that are replicated in the retest session but washed out in the group averages. On the other hand, predictions by the linear regression model missed out the gross topology of activation specific to some contrasts. Overall, BrainSurfCNN’s prediction consistently yielded the highest correlation with the individual tfMRI contrasts, approaching the upper bound of the subjects’ retest reference.

Subject identification

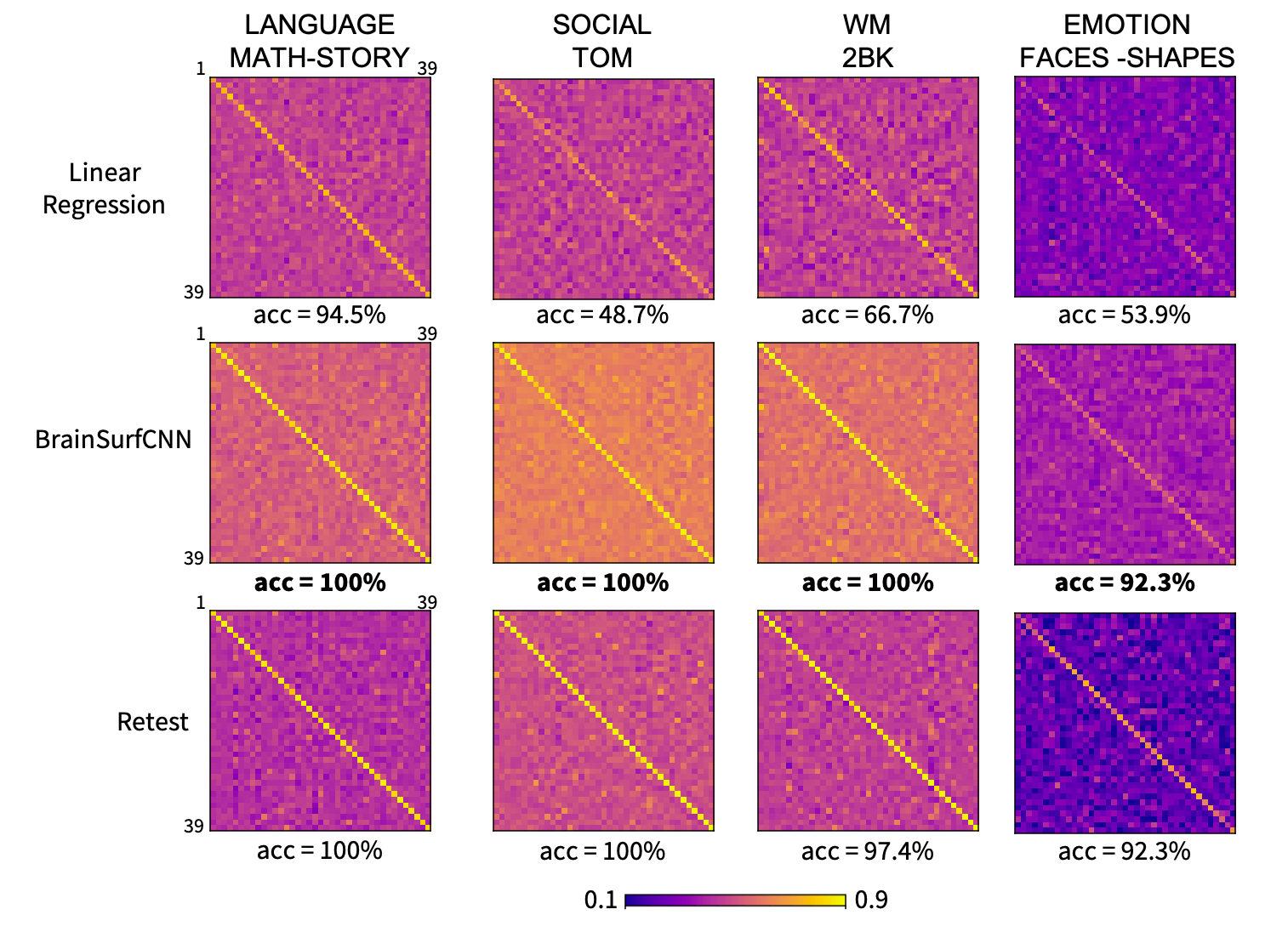Figure 5: Correlation matrices (normalized) of prediction versus true subject contrasts for 2 task contrasts across 39 test subjects.

The matrices were normalized for visualization to account for higher variability in true versus predicted contrasts. All matrices have dominant diagonals, indicating that the individual predictions are generally closest to same subjects’ contrasts.

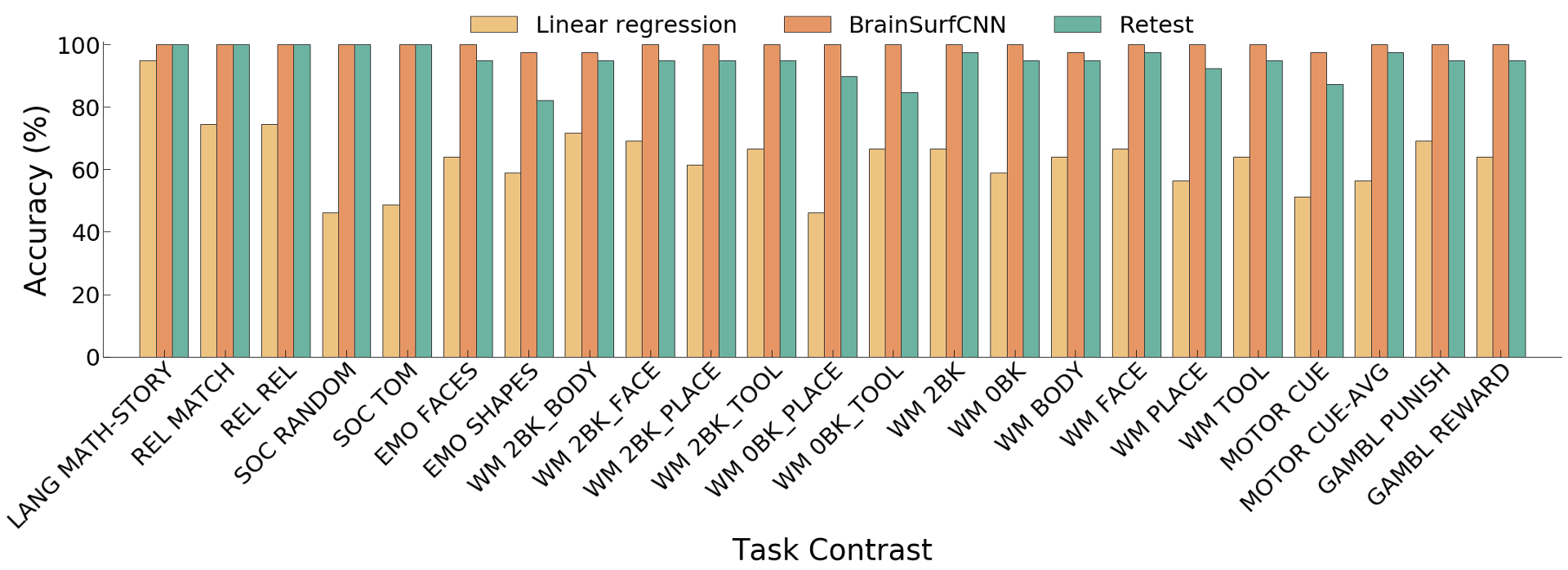Figure 6: Subject identification accuracy of predictions for 23 reliably predictable task

Across all reliable task contrasts, the task contrasts predicted by BrainSurfCNN have consistently better subject identification accuracy as compared to the linear regression model, shown in Figure 5 and the clearer diagonals in Figure 6.

Conclusion

Cognitive fingerprints derived from rsfMRI have been of great research interest (Finn et al., 2015). The focus of tfMRI, on the other hand, has been mostly on seeking consensus of task contrasts across individuals. Recent work exploring individuality in task fMRI mostly utilized sparse activation coordinates reported in the literature (Ngo et al., 2019) and/or simple modeling methods (Tavor et al., 2016, Cole et al., 2016). In this paper, we presented a novel approach for individualized prediction of task contrasts from functional connectomes using surface-based CNN. In our experiments, the previously published baseline model (Tavor et al., 2016) achieved lower correlation values than the group-averages, which might be due to the ROI-level modeling that misses relevant signal from the rest of the brain. The proposed BrainSurfCNN yielded predictions that were overall highly correlated with and highly specific to the individuals’ tfMRI constrasts . We also introduced a reconstructive-contrastive (R-C) loss that significantly improved subject identifiability, which are on par with the test-retest upper bound.

We are pursuing several extensions of the current approach. Firstly, we plan to extend the predictions to the sub-cortical and cerebellar components of the brain. Secondly, BrainSurfCNN and R-C loss can be applied to other predictive domains where subject specificity is important, such as in individualized disease trajectories. Lastly, we can integrate BranSurfCNN’s prediction into quality control tools for tfMRI when retest data are unavailable.

Our experiments suggest that a surface-based neural network can effectively learn useful multi-scale features from functional connectomes to predict tfMRI contrasts that are highly specific to the individual.